GE CHEN†, ZHIXIN LIU† , AND LEI GUO†

†Key Laboratory of Systems and Control, Academy of Mathematics and Systems Science, Chinese
Academy of Sciences, Beijing 100190, China (chenge@amss.ac.cn, Lzx@amss.ac.cn, Lguo@amss.
ac.cn).

This paper investigates the synchronization behavior of a class of flocks modeled by the nearest neighbor rules. While connectivity of the associated dynamical neighbor graphs is crucial for synchronization, it is well known that the verification of such dynamical connectivity is the core of theoretical analysis. Ideally, conditions used for synchronization should be imposed on the model parameters and the initial states of the agents. One crucial model parameter is the interaction radius, and we are interested in the following natural but complicated question: What is the smallest interaction radius for synchronization of flocks? In this paper, we reveal that, in a certain sense, the smallest possible interaction radius approximately equals 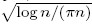, with n being the population size, which coincides with the critical radius for connectivity of random geometric graphs given by Gupta and Kumar [Critical power for asymptotic connectivity in wireless networks, in Stochastic Analysis, Control, Optimization and Applications, Birkh¨auser Boston, Boston, MA, 1999, pp. 547–566].

Society for Industrial and Applied Mathematics Vol. 50, No. 4, pp. 1950–1970. 2012